Data Density and Genetic Algorithms when Playing Solitaire / Playing Solitaire Smart
About three months ago I held a small talk on the benifits of using genetic algorithms to help debug and test code, as well as showing what I think is a fantastic example of how critical data density can be to a system. All of this stemmed from a fairly simple task: Writing a program to play a game of Solitaire.
At the request of people who were not able to attend, this post will go through most of what was covered at the talk.
The task was set by our lecturer as an exercise in functional programming, so all the code referenced below will be in Haskell and the actual functionality of the system will be kept intentionally vague.
The task was split out into two sections. First, we were instructed to implement the mechanics of a game of Eight-Off Solitaire (the Wikipedia article on the game explains it's mechanics quite well), we were then asked to implement a basic AI to play the game through to completion. The most logical way to approach this task - and the way many people did - was to work on those two aspects one after the other; once the game was made, an AI could be made that could play the game well.
Making the Game
The first step was to make the game itself. There were many ways this could be implemented, but here I'll just skim over the general structure one might want to take.
As the wikipedia article explains, there are 3 main features of Eight-Off Solitaire: The foundations; four piles of cards which the player must build up - in suit - from Ace to King in order to win the game, the cells; eight single-card storage locations for cards during play - half of which contain a card at the start of the game, and finally the tableau; arguably the most complex part of the game's setup - consisting of eight columns of (initially) six cards that the player can move cards from or onto as long as they follow suit sequence.
The board itself can be made quite easily with some basic data structures, so the next thing to examine is the actual actions that a player can take. Wikipedia informs us that single cards can be moved from the top of any column within the tableau to to any free cell or the top of a foundation stack or another column within the tableau as long as it's in the appropriate sequence. Again, this is fairly easy to implement, just being a case of writing appropriate move functions between locations. Wikipedia also informs us that:
Technically, one may only move the cards between columns one at a time; however, the presence of a free cell essentially increases the number of cards that can be moved. (e.g., if there are three open cells, four cards can actually be moved at once - one for each cell, and the one that can always be moved.)
Looking at this, we'll make a note that we could implement some kind of batch-movement of cards between columns, but as the feature is derived from moving one card at a time - a feature that we will also be implementing - We'll leave it for now and just write logic that will allow any single card movement from one place to another around the board, as long as it's a legal move. The task also specified that new coloumns in the tableau could only be started using a King, which is listed as a more advanced limit on the Wikipedia page: "Advanced players, however, may prefer to limit this move to Kings only (as it is in Klondike)."
Making the AI
So assuming that we've implemented all that, and with the game mechanics done, we get to move onto the fun bit: the AI! Now, this was specified such that we needed to implement two functions: findMoves and chooseMove where findMoves finds a list of all possible moves that can be made from a given game situation, and chooseMove would choose the most optimal move to make. So naturally, the thing to do is to list every move, rank them, then choose the highest ranked move and make it. Lets see what happens when we run it:
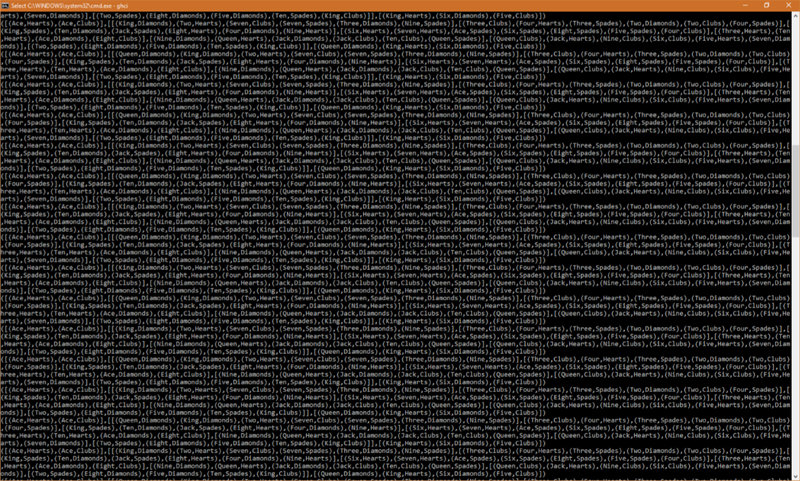
This is not what we wanted to see happening. Looking closer at the output there, we can see that it's just moving the Queen of Diamonds between a column it's sitting on and the reserves every move, and not actually making any sensible moves.
So a little frustrated, but nevertheless determined, we try to fix the problem. The first thing that you will notice seeing this problem is that it will only occur when a card is removed from a column
that is part of a sequence, meaning that - in most cases - the card now placed in the reserves fits perfectly back on the column it was just taken from. Thus, the best choice is to put it back on the column,
resulting in what we see in the picture. The most obvious solution to first try is to put in place procedures that stop the card that is being removed from being part of a sequence, so adding some kind of properlyPlaced
function that, when given a card, works out whether that card has already been properly placed and if so doesn't remove it, something like this:

But alas and alack, all this seems to achieve is a slightly faster route to failure:
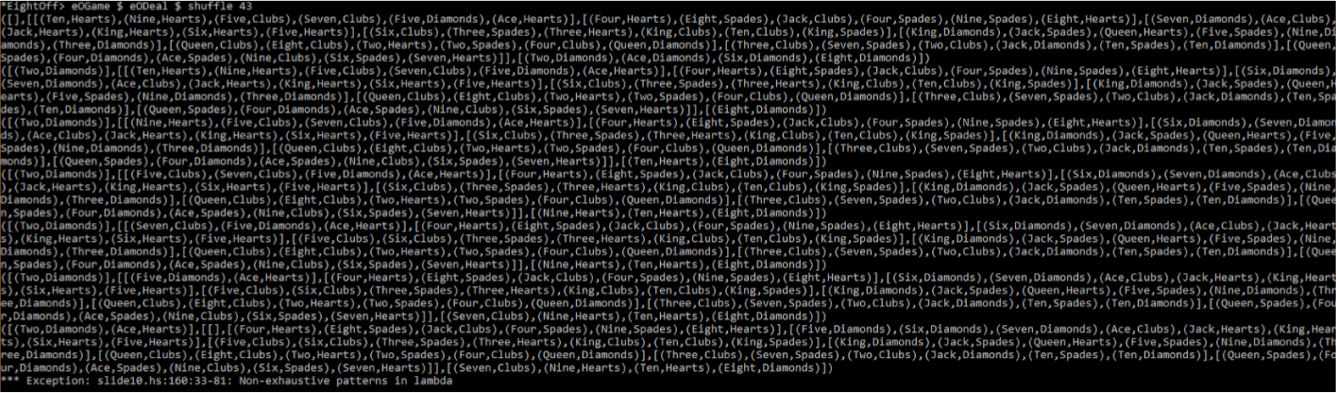
Just adding more and more bits of code isn't cutting it - it's simply exhausting every option we've given it. So what exactly is going wrong here? By this point, we've tried a couple of different ways of ranking the available moves; none of which seem to work all that well, and we can't see an easy fix in sight. What would be really nice, is if we could somehow find the best way of using the data that we have available to us (i.e. the current positions of the cards on the table), and then use that to control the AI.
Enter the Gentic Algorithm
Taking a detour from our woes, we'll look at genetic algorithms. Genetic algorithms are really, really good at optimisation problems (providing that you can present the problem in the correct way, that is). They were first proposed by Alan Turing in the 1950s, and then popularised during the 60s, mostly on the back of papers published by a guy called Alex Fraser.
Genetic algorithms are essentially a way of navigating through a search space by selecting the best solutions to a problem, combining them together and changing them around a bit, then generating more potential solutions, which are then put through the same process. This is essentially mimicing what we know as natural selection in the real world. The 'genetic' part of it's name comes from the fact that every problem proccessed is first broken down to a set of simple weights that effect the outcome of the solution calculation; each set of weights can be thought of as being akin to a gene in a real living being. After many itereations, the best 'gene' is selected and provided as the answer. It may not be the exact best answer to the problem, but it can certainly be close. Below is a video of a genetic algorithm learning how to control a simple simulated agent. It does this by testing each agent on randomly generated race-tracks, and measuring the agent's performance against an estimated average, then using this data to rank each solution:
So what exactly does this have to do with our game of solitaire? Well, as we now have a general way to optimise any problem we can quantify as a set of numbers (a 'gene'), it means that if we can reduce our AI problem down to a gene, then attempt to optimse to the best solution, we might have a shot at making our AI actually play well!
So we go ahead and do that. First, we remove our failed 'properly-placed' constraints, and then for every static variable in the code, we replace it with a reference to a unique part of the gene.
In my case, that involved replacing all static variables with gene!!i, where i is a unique index:

Then, in order to get the genetic algorithm side of things working, I wrote a simple library for Haskell which can be found here.
With this done, we can be quite confident now that our AI is using all of it's available resources to a near-maximum effeciency, so it should be able to play solitaire pretty darn well now! Let's see how it fares:

As we can see, it's doing exactly what it was the first time we tried to implement an AI! It seems that we're all the way back to square one. However, now we are armed with some additional knowledge. Our foray into genetic algorithms has informed us that the solution we currently have must be (or at least there's a high chance it is) playing the game optimally with the information that it's got. But it seems like it's not. This means that there is only one realistically probabable answer: it physically can't. The system must be getting limited information somehow, we must have made an assumption that wasn't true.
And in fact we did.
Remember 14 paragraphs back when I said "we could implement some kind of batch-movement of cards between columns, but as the feature is derived from moving one card at a time - a feature that we will also be implementing - We'll leave it"? That was totally and utterly wrong. There is a major difference between moving a set of cards between columns and moving individual cards at a time. The key to this difference is information density. The AI we have built acts over individual moves, that is it's domain. It looks at a list of moves, ranks them, then chooses the best move and makes it. By adding the ability to move multiple cards in one move, we are effectively expanding the AI's domain, enabling it to effectively have a look-ahead.
Another way of thinking about this is to use a partial finite state diagram, as marked below where each circle represents a state, double circles a completion state, the arrows transisitons, and the red circle the current state of the system:
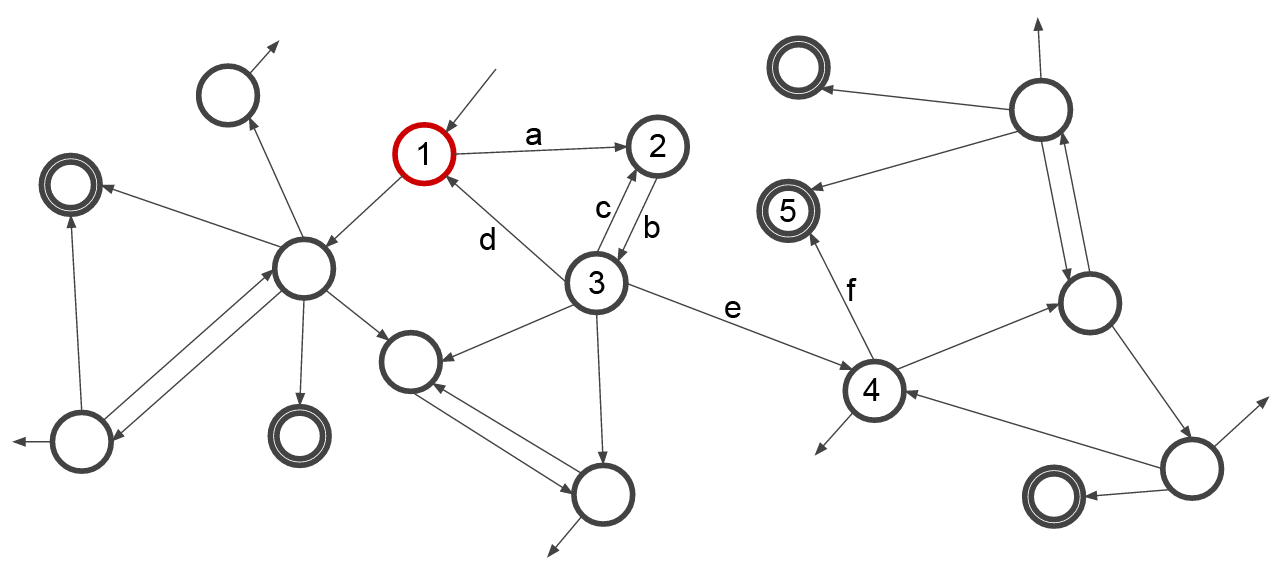
When moving a single card, the AI can only move between one state at a time, so in this scenario, it might move from state 1 to state 2 through transition b, then determine that the next best step would be to move to state 3. But here we see the problem with navigating the state-space like this: at state 3, the AI cannot see that taking transitions e and f would lead it to solution state 5. Instead, it might get to state 3 and choose to transition back through c, and then just continue looping between states 2 and 3 infinitely (as we saw earlier where it just kept moving the same card back and forth).
Now contrast this to a system that can move, in this instance, two cards at a time:
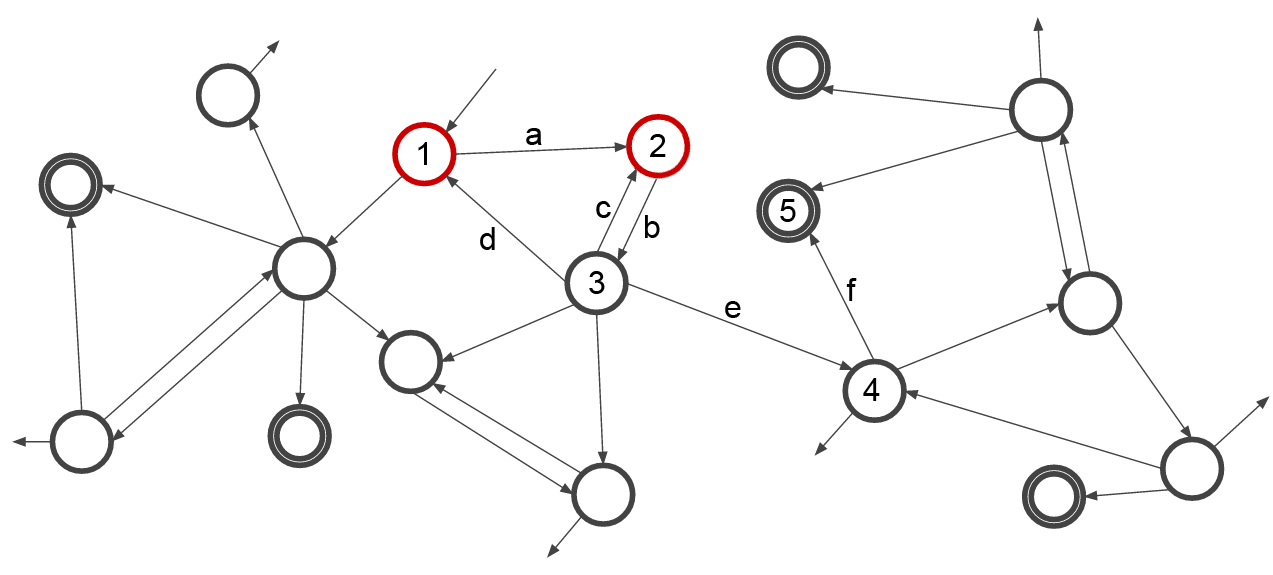
Here, the start state is (1,2), and moving through transition b takes it to state (2,3). Unlike in the single-card setup, this system cannot be caught in the b/c transition loop, as in the (2,3) state, it occupies both states. This means it can then transition through e and f, ending in the solution state (4,5), performing perfectly without getting caught in a loop.
Of course, an AI that could only ever move two cards at a time would fare almost definitely worse than the single-card AI - as there are significantly fewer situations in which a double-card move can be made. However,
summing these two play types together, you end up with an AI that has the choice to move two or one card at any given time, increasing the amount of information it has in order to decide on it's next move. We will
implement it so that any sequence of cards can be moved, dramatically increasing the information density of a move (or the AI's ability to 'look-ahead'). We can also elminate any move that would break a sequence, effectively
brining back in our properly placed function from before, but this time there are moves that can be made in the game that can get the AI to a winning state, so it no longer results in us exhausting our options.
Finally, we can see all our hard work paying off, the system now wins on average ~36 of it's 100 games:
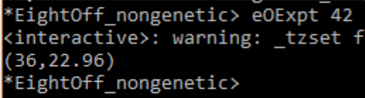
Success at long last! With the additional information, the AI can now play the game properly. Of course, there are other ways of getting this additional information into the system - a history, for example, could be used. More information about the board could be taken into the decision the AI makes, such as how many free slots are left, or the AI could even be run for every decision, and the results of those steps in the future could be used in the next move calculation (a much more traditional look-ahead system).
In the end, I feel that this situation is a fantastic example of just how drastically the infrastructure of a system limits whatever you build on top of it; we couldn't build a good AI without properly building the game mechanics to support it. After all, it doesn't matter how good you are at driving, you can't drive a car that has no wheels. It's also been a great opportunity to use genetic algorithms to debug a fairly abstract system, allowing us to see what it's limits were.
I hope this post has been as interesting to read as it was for me to present those months ago! I'm not entirely sure this translated particularly well from presentation to blog post, but hopefully it was still interesting enough. A big thanks to Moritz Bohm-Waimer for his assistance with proof-reading, without which this post would be markedly harder to read. Feel free to leave a comment or ask a question, and I shall try to respond as best I can. Thanks for reading!
